What are triangles?
Triangles are polygons with three sides and three angles. The sum of the three angles in any triangle is always 180 degrees.
- A triangle with sides measuring 4 cm, 5 cm, and 6 cm
- A triangle with angles of 60°, 60°, and 60°
Every triangle, no matter its size or shape, always has three sides, three angles, and the angle sum of 180°.
Types of triangles by angles
Triangles can be classified based on the size of their angles. The three main types are acute, right, and obtuse triangles.
- Acute triangle: All three angles are less than 90°.
- Right triangle: One angle is exactly 90°.
- Obtuse triangle: One angle is greater than 90° but less than 180°.
Every triangle fits into only one of these categories based on its angles.
Acute triangles
An acute triangle has all three angles measuring less than 90 degrees. The angles are sharp and narrow.
- A triangle with angles 50°, 60°, and 70°
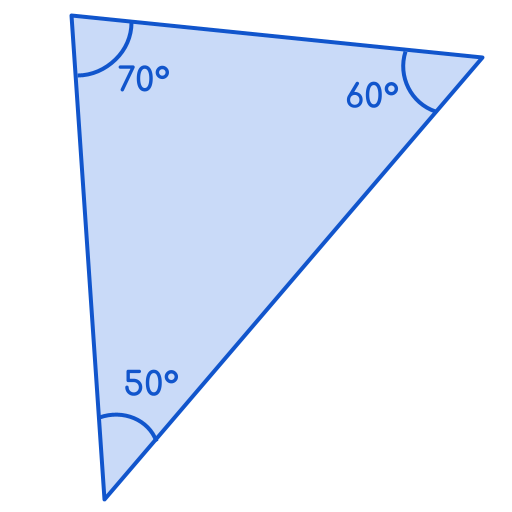
If every angle in a triangle is small and less than 90°, it is an acute triangle.
Right triangles
A right triangle has one angle that is exactly 90 degrees. The side opposite the right angle is called the hypotenuse.
- A triangle with angles 90°, 50°, and 40°
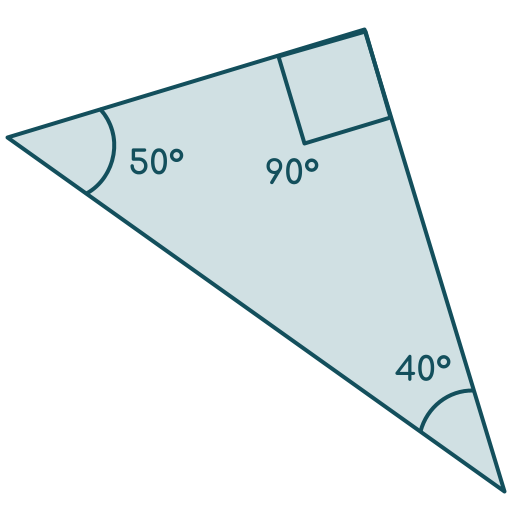
Right triangles are common in real life — they are used in building corners, ramps, and roofs.
Obtuse triangles
An obtuse triangle has one angle greater than 90 degrees but less than 180 degrees. The other two angles are always acute.
- A triangle with angles 100°, 50°, and 30°
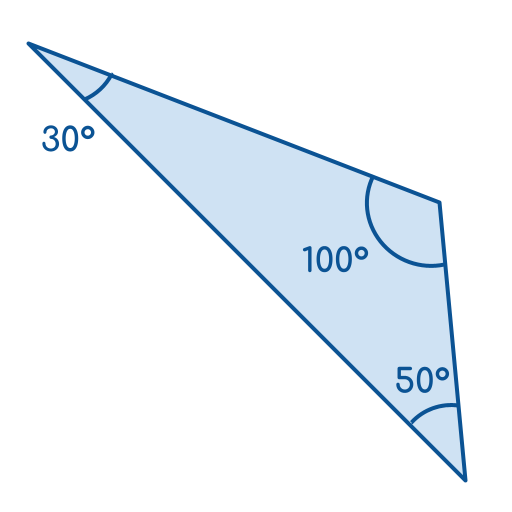
A triangle can have only one obtuse angle because the sum of all angles must be 180°.
Comparing acute, right, and obtuse triangles
Each type of triangle has a different kind of angle. Knowing these differences helps identify triangles quickly and accurately.
- Acute Triangle: All angles < 90°
- Right Triangle: One angle = 90°
- Obtuse Triangle: One angle > 90°
When identifying a triangle, always look for the largest angle first — it determines the triangle’s type.
Real-world connections
Triangles are used in art, construction, engineering, and design because of their strength and stability.
- Bridge supports use right triangles for balance.
- Roof trusses often include acute and obtuse triangles for structure.
Recognizing different triangle types helps you understand geometry in everyday objects and designs.